月は8.85年で、近地点が一周する
月は、3,232.6054日(8.85年)で近地点が一周移動します。(1年で約41度)
太陽に近い水星が、100年で575秒程度しか近日点が移動しないことと比較すると、
かなり大きな近点移動になります。
水星の近点移動の原因の大半は、
惑星の重力による摂動とされています。
摂動で説明できない、43秒は、
アインシュタインの相対理論で証明されました。
月に関しては、
地球の質量が宇宙空間の歪みで
月の軌道を変えるほどの影響はないため、
摂動で1年41度近点移動していることになります。
国立天文台の説明によると、
「月の楕円軌道の向きは一定ではなく、太陽の影響により周期約8.85年で回ります。」
とあります。
しかし、太陽の影響が太陽と月の方向とは異なる進行方向に
大きく働くのは少し無理があります。
そこで、楕円軌道の理論による、
「円軌道」の公転周期と「振動」の振動周期の差により、
近地点移動が発生するという考え方で、近地点移動を考察します。
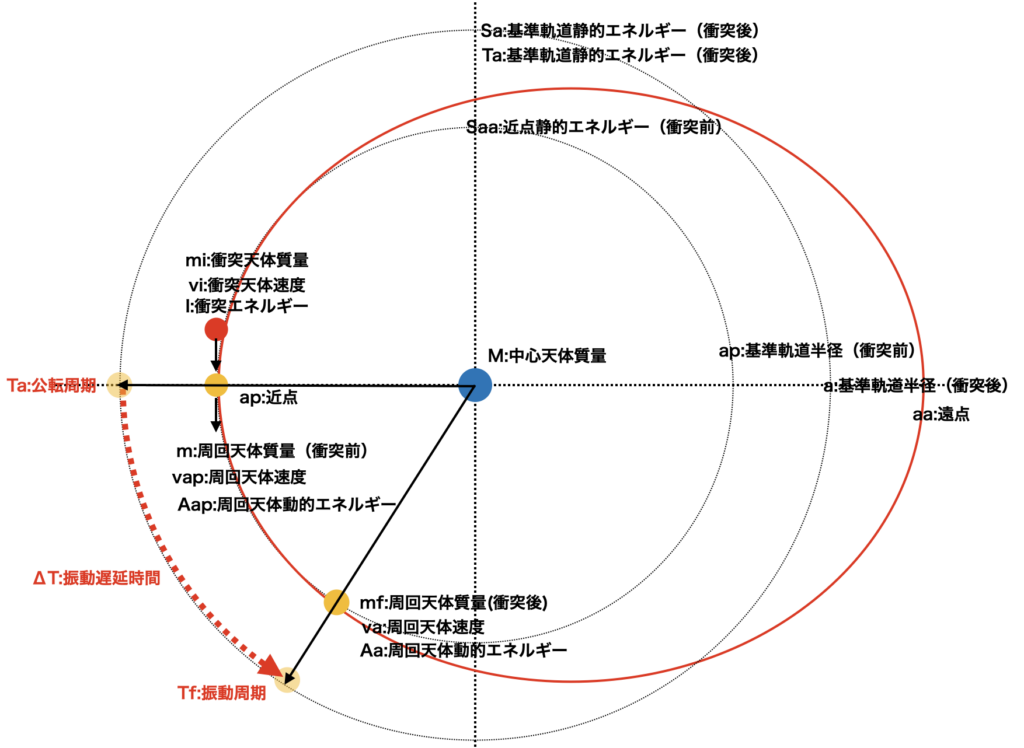
公転周期と振動周期
質量変位とは、衝突時に周回天体の質量が変化することことです。
公転周期と振動周期は次の表の様になります。
| 衝突後の質量 | 公転周期 | 振動周期 |
| 増える | 変わらない | 遅くなる |
| 減る | 変わらない | 早くなる |
公転周期は、「基準軌道上」を一周するする時間です。
振動周期は、衝突により、基準軌道を中心に近点と遠点を振動する周期です。
この振動周期が、変化すると、公転周期との間に差が発生し、それが、近点移動の原因となります。
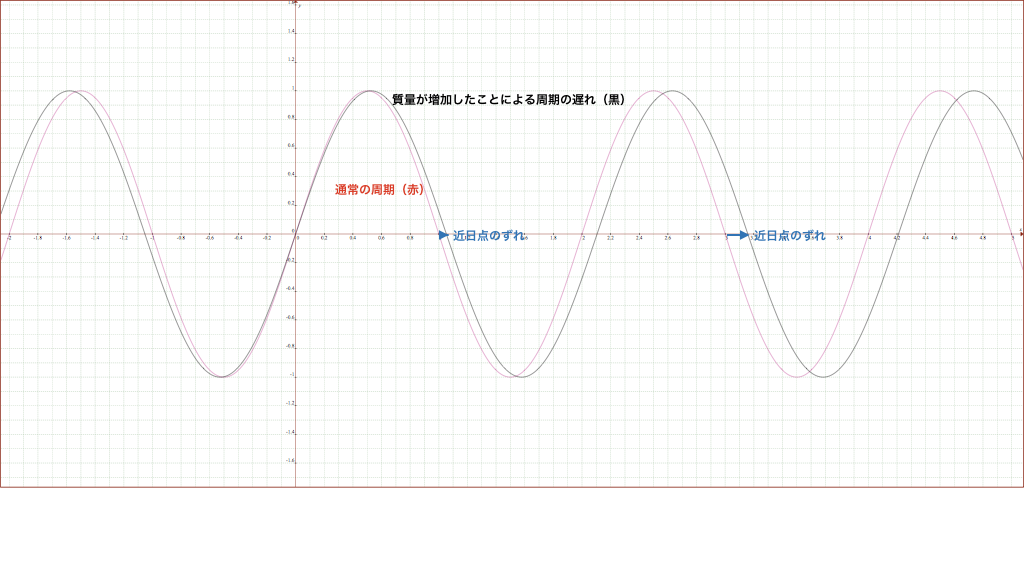
下の図は、衝突によって、公転周期と比較して、振動周期が増えたグラフを表しています。
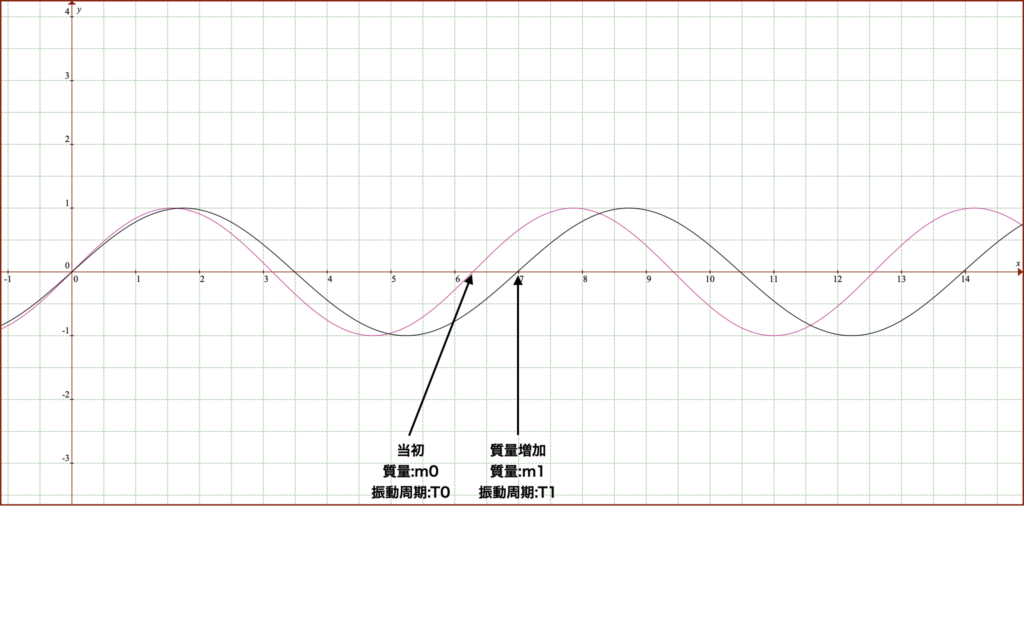
次の図は、質量が変化によって近点が移動したグラフです。
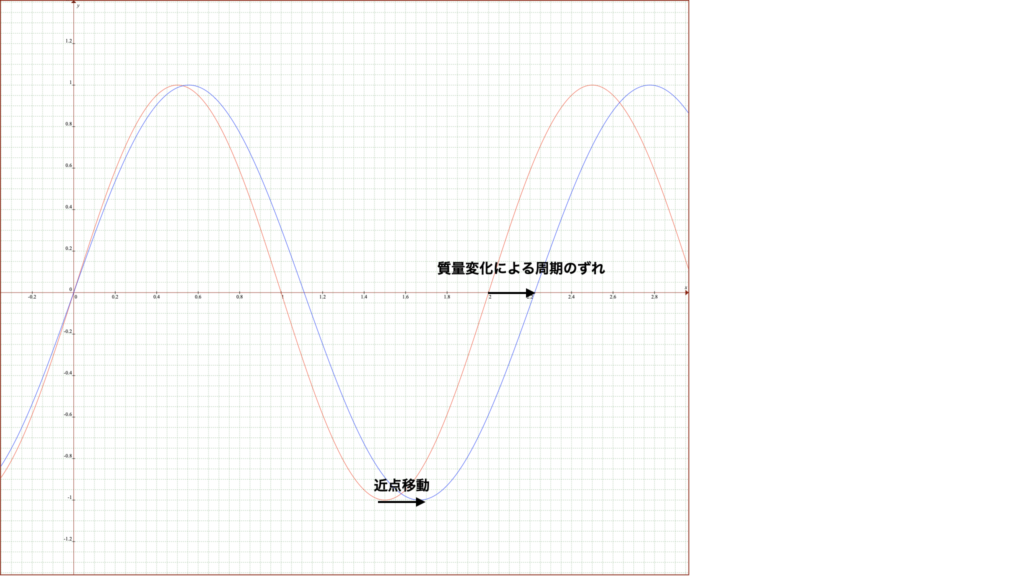
周回天体(m0)がΔm増加した場合の質量(m1 = m0 + Δm)の時の振動周期の変化は、
基準軌道を中心として、バネ係数kの周期と同じになるので、
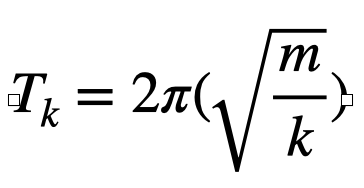
となります。
バネ係数kは、基準軌道半径(a)と位置(a)の静的エネルギー(Sa)を使って、
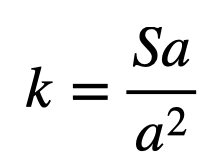
で表すことができます。
楕円軌道は、
公転周期と振動周期の2種類の周期が存在します。
公転周期と振動周期が同じ場合、
衝突したところと同じ位置に戻ってきますので、
近地点(または遠地点)は移動しません。
しかし、振動周期が変わった場合を考えて見ると、
近地点の位置が元の位置とは違う位置になります。
振動周期が遅くなれば、近地点は元の位置より前へ、
早くなれば、近点は元の位置より後ろへ移動することになります。
近地点移動は公転周期と振動周期の位相差
振動周期ωsは、バネ定数kと質量mを使って
と表されます
この式からすると、質量が変化することによって、振動周期が変わります。
グラフにするとこんな感じです。
近点移動しているときの質量mf は、
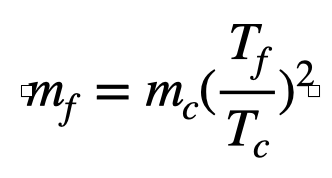
この式で算出できます。
証明は、

公転周期と、振動周期が求まれば、質量が簡単に算出できます。
1周する時の近点移動の角度Δθ
実データで計算(月の近点移動)
小惑星が現在の近点の位置(ap=356;400km)で円軌道上を動いている月に衝突して、基準軌道が(a=384,400km)になったケース
【基本データ】
| 項目 | 値 | 備考 |
| 宇宙エネルギー定数 | U = 7.42426E-3 km/kg | FIX |
| 光速 | c = 1.07925E+9. km/h | FIX |
| 中心天体質量 | M = 5.97219E+24 kg | 地球質量 |
| 周回天体質量 | m = 7.34767E+22 kg | 月質量 |
| 基準軌道半径 | a = 384,400 km | |
| 中心天体からの衝突位置 | ap = 356,400 km | 近点衝突 |
| 月半径 | R = 1,738.2km | |
| 月密度 | ρ = 3.34E+12 kg/km3 | |
| 周回天体質量エネルギー | Em = 1.16479E+38 je | |
| 光速時基準軌道半径 | ac = 0.00141 km | |
| 1公転誤差角度 | deg1 = 10,948.15003 秒 | 8.85年/周 |
| 円周秒数 | CsS = 1,296,000 秒 | 360° x 3600秒/度 |
| 年間時間 | CyT = 8,760 時間 | 365日 x 24時間 |
【結果】
| 項目 | 値 | 計算式 |
| 基準軌道(a)静的エネルギー | Sa = 9.99332E+29 je | Sa = Em x (ac / a) |
| 基準軌道(a)公転速度 | va = 3,687.9 km/h(1.0km/s) | va=√(Sa / m) |
| 基準軌道(a)公転周期 | Ta = 654.91225 h | AHr = 2 x π x a / va |
| 周回天体1周の公転周期遅延 | ΔT = 5.53247 h | ΔT = deg1 / CsS × Ta |
| 衝突後の周回天体質量 | mf = 7.47234E+22 kg | mf = m × ( (Ta + ΔT) / Ta )^2 |
| 衝突による質量増減 | Δm = 1.24665E+21 kg | Δm = mf – m |
| 衝突エネルギー | I = 7.8511E+28 je | I = Sap – Sa |
| 衝突天体の質量 | mi = 4.98662E+21 kg | 予想(Δmの4倍設定) |
| 衝突天体の半径 | ri = 709.0 km | ri = ( mi / ( 4/3 × π × ρ ) )^( 1/3 ) |
| 衝突天体の相対速度 | vI = 3,967.9 km/h(1.1km/s) | vI= sqrt( abs( I ) / mi ) |
| 衝突天体衝突速度(中心天体に対する) | Δv = 7,797.9 km/h(2.2km/s) | Δv = vap + vi |
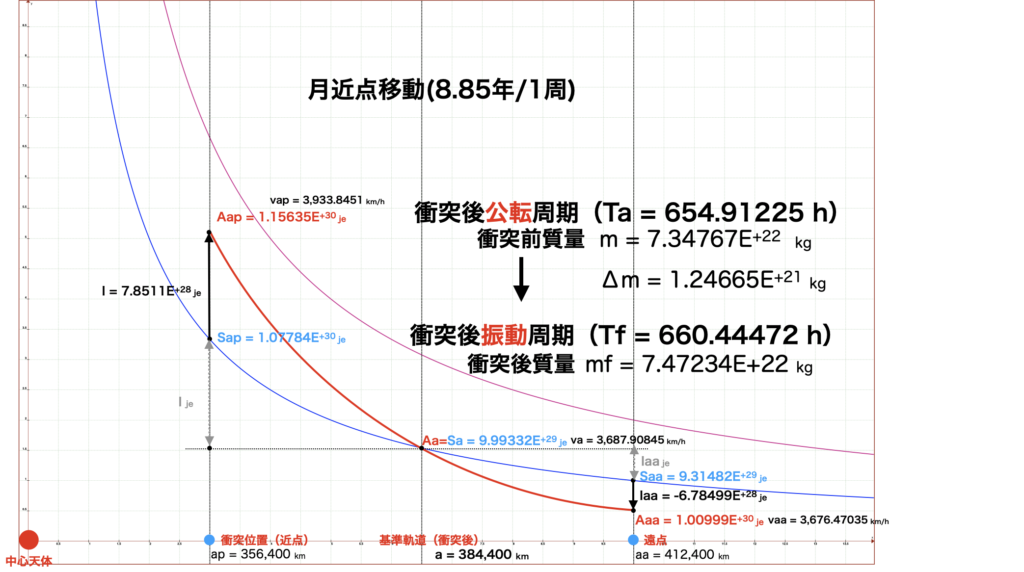
地球から、356,400kmの位置で、月(質量m = 7.34767 x 10+22 kg)に、
半径約700Kmの小惑星が秒速2km/Sで衝突して、
基準軌道が、384,400kmに移動して、
質量がmf = 7.47234 x 10+22 kg(1.25 x 1021kg 程度増加)になると
8.85年で近点が一周する近点移動することがわかります。
わった時に振動周と公転周期が異なり、
近点移動を始めます。
この理論は、彗星でも月でも他の惑星にも当てはまり、
どの位置で(遠点または近点)、どんな大きさの天体が衝突したのかがわかります。
近点か遠点かは、予想するしかないところではありますが、
衝突速度などをみればある程度の想像はつきます。
水星でもこの理論が成り立つので、
アインシュタインの一般相対性理論の証明の一つ、
「水星の近日点移動」の推論は、質量変異の方法でも成り立ち、
近点移動については、もう少し、見直す必要があるのではないかと思います。
ちなみに他の惑星の近点移動でも、ためしてみましたが、
ある程度納得のいく結果を得ることができました。

