そもそも、三体問題(多体問題)はニュートンが「万有引力」なるものを提唱したために、考えなければならなくなってしまった。「引力」はともかくとして、「万有」なのかというのが、ポイントとなる。「万有」がゆえの摂動なのだから。(みつお!?)
まず、天体の動きを力で考えるのは無理がある。もし太陽が地球を引力でひっぱているとする。太陽のどの部分が地球のどの部分を引っ張っているのだろうか。考えるだけで複雑怪奇でどういう式を立てていいかわからないのである。力を球面に沿って積分していくのか?
結局太陽の中心が地球の中心を引っ張っているという結論で納得させられたのも事実である。ロープでつながっているならともかく、どう考えても納得がいかない。
アインシュタインが登場して、重力は時空の歪みだ!ということになった。しかし、それも納得がいかない。水星の近日点移動の摂動以外の43秒がアインシュタインの一般相対性理論で解けたのではあるが、もとを辿れば、摂動の計算はかなり複雑なはずで(わたしは思いつかないが)、それ自体本当に合っているのか疑問である。
そこで、考えたのが二体問題しか発生しないということである。そうすれば、多体問題は考える必要がなくなるし、摂動もなくなる。さらには、摂動がないのだから、水星の近日点移動の43秒も考える必要がない、ということは、アインシュタインの一般相対性理論も怪しいということになる。
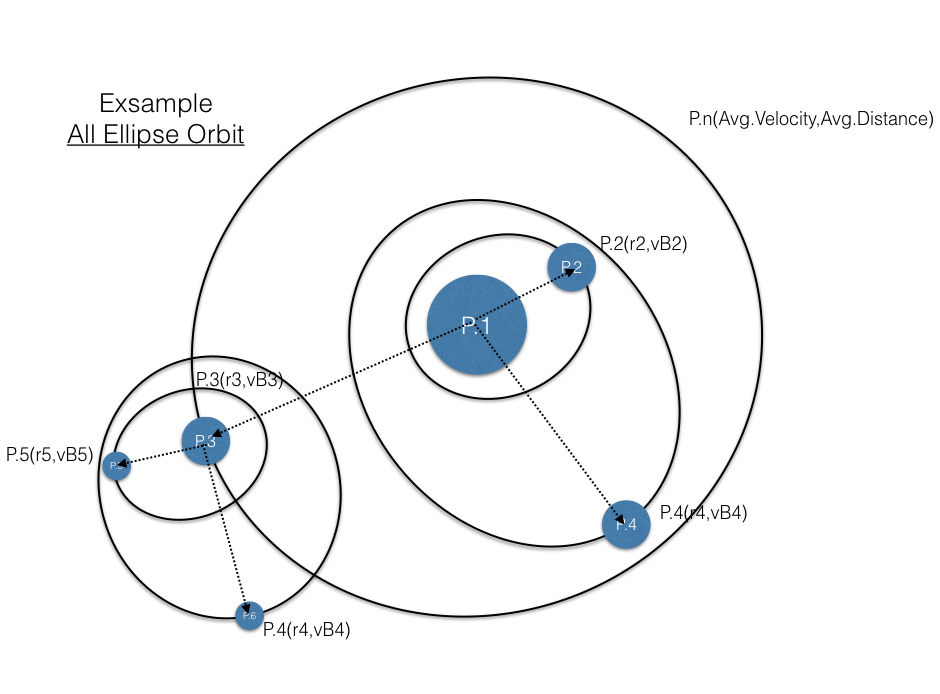
ニュートンの考え方は、全ての物体が引力で引き合っている、いわゆるネットワーク構造をしているということだ。このネットワーク構造が複雑で三体以上になるとうまく解けない。そこで、すべての天体は親と子の関係になっている構造を考えた。これは、ツリー構造をしており、親のの挙動に子は追随して付いてくる構造である。たとえば、太陽は銀河の周りを回っているが、太陽の周りを回っている地球は、太陽の動きを考えなくてもよい。あたかも、太陽のトラックの荷台に乗って動いている。と考えられる。これはガリレオが提唱した慣性の法則に似ている。ここでは、「軌道慣性」と呼ぶことにする。この関係で1番のポイントは、「親判定」である。子供の親は誰かということである。
仮に宇宙に3天体あったとする。この親子関係を決めることが、すべては似たい問題で解くことができる。親判定1番目の要素は、「質量」である。「質量」が大きいほうが親となる。だから、3体の内質量の一番小さいものは、必ず子となる。そして、一番質量の多い天体は必ず親になる。また、中間の質量の天体は一番大きな質量の天体の字となる。問題は質量の一番小さな天体の親が中間の質量の天体なのかどうかという点である。
親判定の2番目の要素は、親となりうる天体からの子の位置aにおける「静的エネルギー(Sa)」と子の天体の「動的エネルギーA」の大小関係である。たとえば、子の動的エネルギーAが、中間の質量の天体のSaの2倍以上ある場合は、親は一番大きな質量の天体になる。また、子の動的エネルギーAが、Saの2倍未満なら、中間の質量の天体が親になる。
親判定により親が一意に決まるので、3天体はツリー構造になる。もう少し詳しい説明は後日おこなう。
