なんと、気がつけば6月もまじか、前回ブログを書いたのは、4月だった。
時の経つのは早いもので、コロナと戦いつつ、在宅ワーク。
在宅ワークも、エコノミー症候群を発症しそうなくらい、椅子に座っている。
結局一日うちにいるから、部屋は散らかり放題。
こんな生活、誰が想像しただろうか!
そんなこんなで、1ヶ月「双曲線軌道」について考えていたのですが、
まあ、仕事をしろ!ってことかもしれませんが、そこは大目に見て。
双曲線軌道をなんとかエネルギーで解こうとしました。
前にも、ブログとかページに載せてはありますが、
個人的に気に入らない箇所があってそれを解明しようと、
飯も食わずに考えておりました。
というのは全くの嘘ですが。
気に入らないところというのは、
初期値です。
宇宙船は、インテリジェントにエネルギーコントロールしながら、
宇宙空間を進んでいくのですが、
まあ、ここまでは、このサイトで証明してありますので、
詳細は語りませんが、お許しを。
今までの初期値は、
(1)宇宙船の動的エネルギー(AR)
(2)影響圏に入る時の、基準軌道に対する入射角(θ)
(3)近点(r)
の3項目でした。
この(3)近点が気に入りません。
そこもなんとか、(1)(2)だけで出ないものかと、
四苦八苦
それを考えて、早2ヶ月。
いまだに、解明できておりません。(汗)
双曲線の式は、
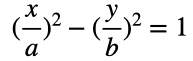

東大塾長の理系ラボから引用
です。
a,b,と焦点距離(c)の関係は
a2 + b2 = c2
です。
ピタゴラスの定理からですが、
そんなことは、わかるわ!ってことですよね。
近点(r)は、上図のa と F(c,0)の距離なので、
c – a
で求まります。
そして、
aは、前述の
(1)宇宙船の動的エネルギー(AR)
(2)影響圏に入る時の、基準軌道に対する入射角(θ)
から求めることができます。
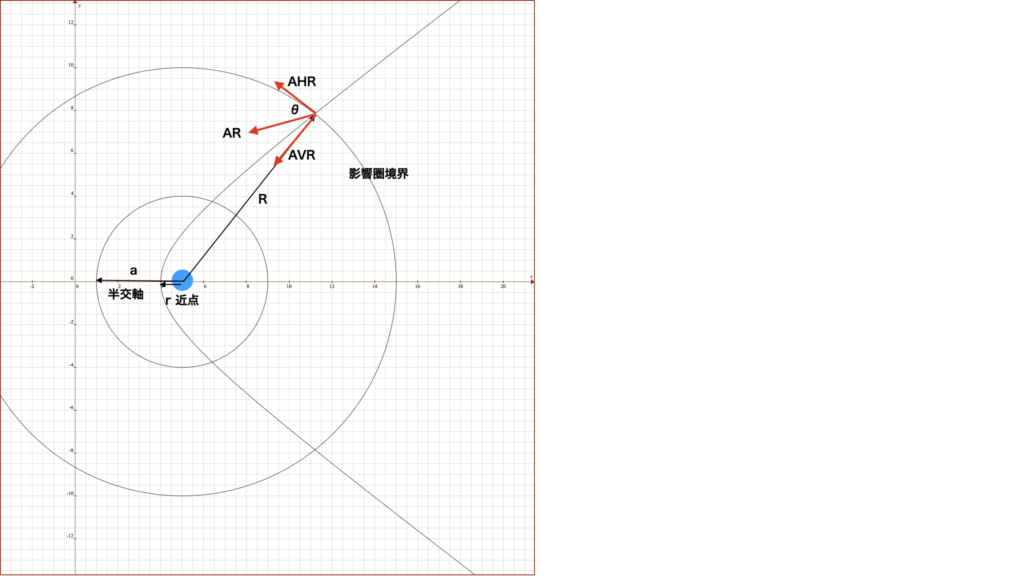
影響圏突入した、中心星からの距離をRと仮にします。
そこでの、宇宙船の動的エネルギーをARとします。
そして影響圏への入射角をθとすると、
中心天体方向のエネルギー(AVR)は、
中心天体からaの基準軌道の静的エネルギー(Sa)になります。
これは、影響圏突入時の距離Rでの、
基準軌道方向の動的エネルギー(AHR)、
中心天体方向の動的エネルギー(AVR)、
基準軌道の静的エネルギー(SR)、
基準軌道の静的エネルギー(Sa)より
AR = AHR + AVR = 2SR + Sa
なので、
AHR=2Sr
AVR=Sa
となります。
エネルギー面積(EA)は、
宇宙船の質量エネルギー(Em)と
光速時軌道半径(ac)
で求まりますから、(なんで〜と思われるかもしれませんが、スルーで)
半交軸(a) = EA / Sa
影響圏突入時の距離(R)=EA / SR
で求まります・
ここまでは、OKfです。
ところが、bを求めるためには、cがわからないと求まらりません、
そして、c を求めるには、bがわからないと求まらないという、
無限ループ。
ブラックホールじゃないんだから、
出てこいやー
と言いたいところですが。
いくら呼んでも出てきません。
あ〜ここまでか。
と、解明に向け続きを考えることにします。
