楕円軌道

軌道モデリング理論

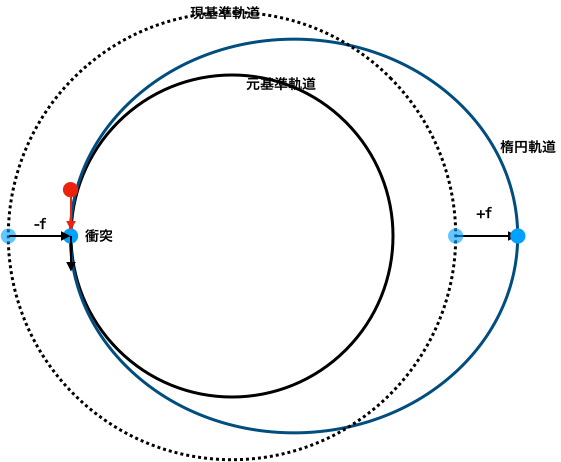
元基準軌道上で衝突すると、
元基準軌道上の円軌道に移り、
そこを中心に±fの単振動の移動をします。

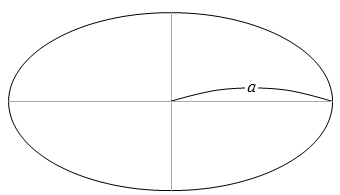
ケプラーの第一法則では、
楕円軌道の長半径を使用して
います。

　楕円軌道について

楕円軌道の原因は、天体同士の衝突です。
衝突により、平均軌道（基準軌道）が変わり、軌道周期が変化します。
衝突後の基準軌道半径と衝突前の基準軌道半径の差が振幅となります。
衝突後の基準軌道を中心に単振動が起こります。
また月が、一周回ってくると元の位置に戻ってくるので、
軌道周期と単振動周期が同じになります。
ケプラーの法則のように、円軌道は楕円軌道の特殊な軌道ではなく、
円軌道が基準で、その円軌道に対して、単振動して楕円軌道にみえるということになります。

円軌道（基準軌道）

基準軌道は、等速円運動をしています。
軌道周期（T）は、基準軌道半径aと軌道平均速度 v を使って

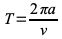
 で求まります。
ここで、基準軌道半径 aは、楕円軌道速度などで使用されている、
楕円軌道の長半径と同じ値になります。
つまり、ケプラーの第一法則のように、
月の軌道は楕円軌道の中心からの長半径aの楕円軌道ではなく、
地球を中心として基準軌道半径aで「円軌道」で周回していると考えても差し支えありません。

「単振動」

月軌道は楕円軌道です。楕円軌道になる原因は、
他の小惑星と衝突した後の基準軌道移動とそこを中心とした「単振動」になります。
単振動の周期は軌道周期と同じとすると、
ある振幅Aで基準軌道aを中心に±Aの振動をする頃になります。
もしも、進行方向と同じ方向に小惑星が衝突したとすると、
当初は基準軌道半径a-Aの円軌道上を月が動いていて、
衝突後、基準軌道がaに変わって、aを中心とした単振動になり、
見かけ上楕円軌道になります。
また逆に進行方向とは逆に小惑星が衝突したとすると、
当初はa+Aの円軌道上を動いていたことになります。
惑星が衝突することによって、円軌道が大きさの違う円軌道に変わって、
変わった距離が振幅となり、単振動して楕円軌道になります。