素数について
そもそも、
素数って何かは、小学校の頃に習っているので、わかっていると思いますが、
1と自分自身の数字でしか割り切れない正の自然数です。
1は素数ではありません。までは定義なので、
そうかと思わざるを得ないのですが。
具体的には、
2、3、5、7、11、13、17、19、23…と続きます。
また、素数の分布について、「リーマン予想」という有名な予想がありまして、
「リーマンゼータ関数の零点が、負の偶数と、実部が 1/2 の複素数に限られる」という予想です。
このリーマン予想が証明されれば、
この気まぐれな素数の並び方に何らかの大切な意味が隠かくされていることが明らかになる。
と言われています。
(どうしてかは、私にはわかりませんが)
それどころか、素数は大宇宙が従う自然法則に関わる創造主の暗号ではないか。
と考える人さえいます。
ということで、
素数は宇宙に関係あるのではないかということで、
少し取り上げてみます
。ζ関数(ゼータ関数)やリーマン予想については、専門書を読んでいただかないと、
私の拙い知識では、説明できませんので。
素数について、もう少し語ると、
最近は暗号化技術の中で使用されています。
それは大きな数の素因数分解は難しいというところから、
鍵として使われています。
簡単に言うと、Aさんが鍵3を持っていて Bさんが鍵5を持っているとします。
Aさんが暗号化キー15を送ったすると、Bさんは鍵5で割ってAさんの鍵が3てわかります。
実際は桁数がすごい多い数を使うのですが。
2018年12月現在で知られている最大の素数は、
2018年12月に発見された、
それまでに分かっている中で51番目のメルセンヌ素数 282589933 − 1 で、
十進法で表記したときの桁数は2486万2048桁になります。
気が遠くなりますが。
素数の判定法
与えられた自然数 n が素数であるか合成数であるかを判定するためのアルゴリズムが多数考案されています。
最も素朴な方法は、2 から √n 以下の素数まで順番に割っていく、
試し割りと呼ばれる方法です。
n が √n 以下の全ての素数で割り切れなければ n は素数である。
試し割りは、n が大きくなるに従って、急速に速度が低下するため、
実用的ではありませんが。
任意の数に適用できる試し割りよりも高速なアルゴリズムが考案されています。
また、特殊な形をした数に対してはより高速なアルゴリズムも存在します。
素数判定は、与えられた数が素数であるか否かだけを判定するものですが、
素因数分解とはより強く、
与えられた数の全ての素因数を列挙することでもあります。
ほぼほぼ同じ要領のエラトステネスの篩(ふるい)があります。また、他の判定法としては、
ウィルソンの定理 ― p が素数ならば (p − 1)! ≡ −1 (mod p) が成り立つ。
逆に、整数 p > 1 に対し、(p − 1)! ≡ −1 (mod p) ならば、p は素数である
最大公約数 ー 2つ以上の整数 の最大公約数が1 であるとき、 は互いに素であるという。
公約数は最大公約数の約数である。
ミラー–ラビン素数判定法、AKS素数判定法 などあります。が、よくわかりません。汗
そこで、自分なりの判定法を考えてみました。
ENDY素数判定法
Pn(素数)までの全ての素数がわかっている時、
どこまでの素数が判定できるかという事を考えてみます。
ゾーン1:2からPnの素数は判定済です。
ゾーン2:Pn+1からPn+1^2(非素数) までの数は「判定可能」です。
ゾーン3:Pn+1^2+1 より大きい数は「判定不可能」です。
というゾーンに分かれます。
ゾーン2の判定方法は嗣のように定義します。
f(Pn)=Πsin(πPn/n) n=2,3…Pn+1 → f(Pn)≠0…素数 、f(Pn)=0…非素数
Pn=5をグラフ化すると
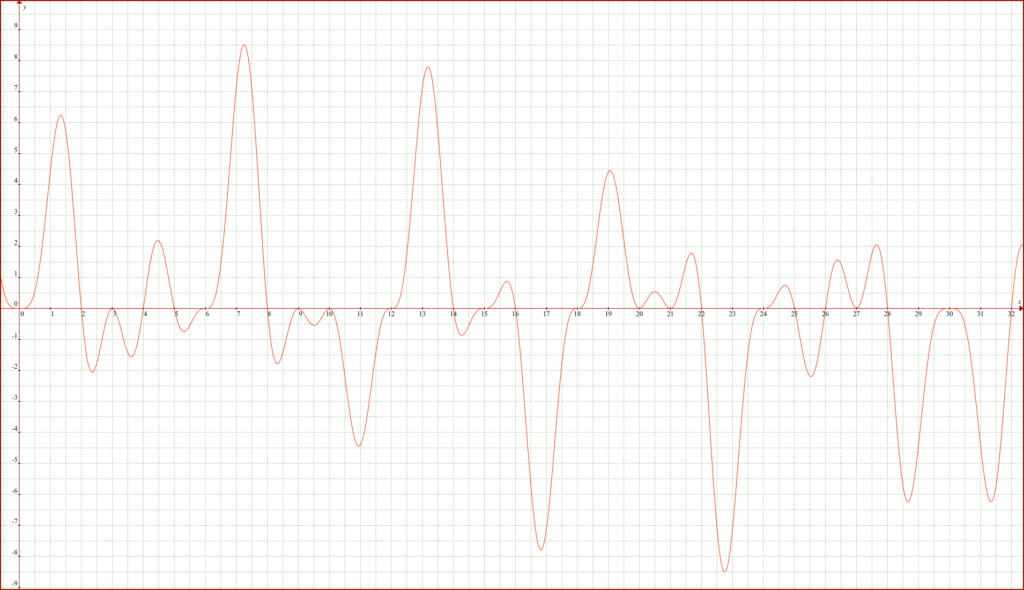
となります。グラフの5より大きいゼロでない数(7、11、13、17、19、23…)が素数になります。確実に判定できるのは7の二乗の49(非素数)までです。
その範囲を判定可能領域と呼びます。
この方法は、素数の可視化が簡単ですが、
欠点は、サインを使用しているため、
コンピューターで計算するとフーリエ展開の誤差でうまくゼロにならないところです。
また桁数が大きくなると、グラフが限りなくゼロに近づいていくので、
拡大する定数を掛けないとならないところです。
しかし、理論的には、一つの公式で素数が判別でき、
判定可能領域の素数の数が把握できます。ということは、判定可能領域ごとの素数分布を捉えることが可能ということです。素数の分布を調べてみたので、したのグラフに表す。右側の数字は、その近辺の素数分布率(素数/実際の数字の数)です。
10の場合、Pn=3、次の素数5の二乗25なので 9から25が判定可能範囲なので、その範囲の素数の5個を数えてます。(9から25) 母数に9は含みません。5÷ 16 =31.25
100の場合、Pn=7、次の素数11の二乗の判定可能範囲49から121
1000の場合、Pn=31、次の素数37の二乗の判定可能範囲961から1369
10000の場合、Pn=97、次の素数101の二乗の判定可能範囲9409から10201)
1000000の場合、Pn=997、次の素数1009 の二乗の判定可能範囲994009から1018081
10000000の場合、Pn=3137、次の素数3163 の二乗の判定可能範囲9840769から10004569
でサンプリングしました。
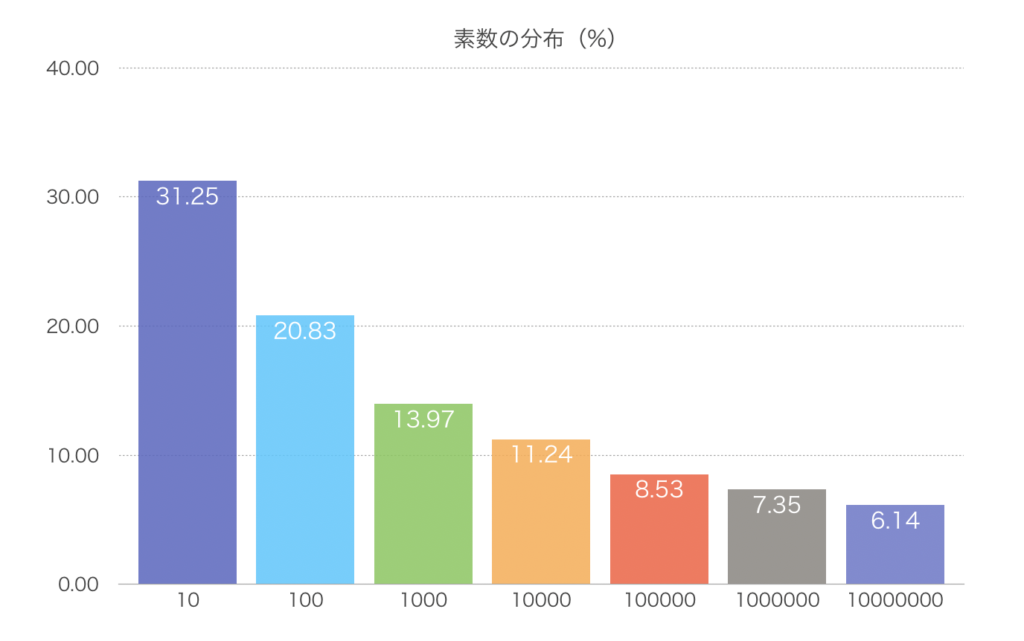
例えば、1,000,000の場合、
1,000の一番近くの素数997の二乗と1009の二乗の間にあります。
Pn=997が決まれば、1,000,000近くの素数の数が分かります。
グラフを見る限り数が大きくなればなるほど、判定可能範囲の数は減っていきます。
さらに大きな数になれば、判定可能範囲は広くなりますが、素数は減ってくるはずです。
ところが、素数は無限にあることは証明されているので、
0%にはならず、有限なところで収束するはずです。
どこか漸近線があるのではないかと推測できます。
限りなくゼロに近づくのでしょうか。
宇宙の構造と素数の因果関係は、
まだ分かりませんが、なんとなく静的エネルギーの減少(Sa=EA/a)に似ている気がします。
何の証明もしていませんが。
遠ざかるほど小さくなるところが。
本質的なところでは、まだ分かりません。
上の素数分布のPythonのプログラムを参考に載せておきます。
