非重力理論からの宇宙構造　

前ブログで、月軌道から「非重力理論」もとい、「重力ないんじゃねえ」の説明をしました。

要するに、エキセントリックな月軌道は、太陽の影響でなくて、二重衝突で説明できるから、あえて重力（ニアー引力）がなくても、エキセントリック軌道になるよ。と言うことでした。では、宇宙構造がどのようになっているかを、どのように説明したらいいかと言うことで、ケプラーの法則を見直してみることにしました。

宇宙構造

ケプラーの第３法則は、惑星の公転周期(T)の２乗は、軌道長半径(a)の３乗に比例する。です。

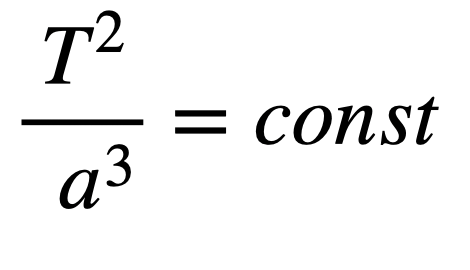
公転周期Tは軌道平均速度vより

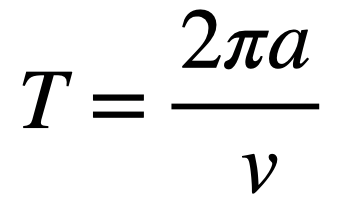
より

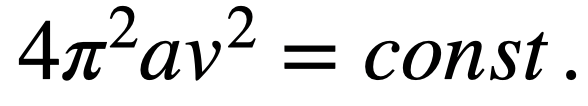
となります。また、vが光速cの時の基準軌道半径をa_cとすると

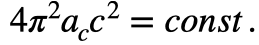
が成り立ちます。

この２つの式の比をとると

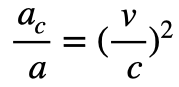
となります。これはケプラーの第３法則の変形です。この式は実際の宇宙構造として扱えます。これを「宇宙構造」と呼ぶことにします。

宇宙エネルギー構造

宇宙構造の両辺に、アインシュタインの質量エネルギー変換式を質量エネルギーと呼ぶことにします。

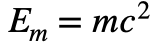
を両辺にかけると、宇宙構造の両辺がエネルギーになり、両辺のエネルギーがバランスすることになります。

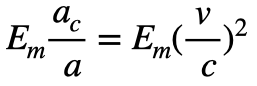
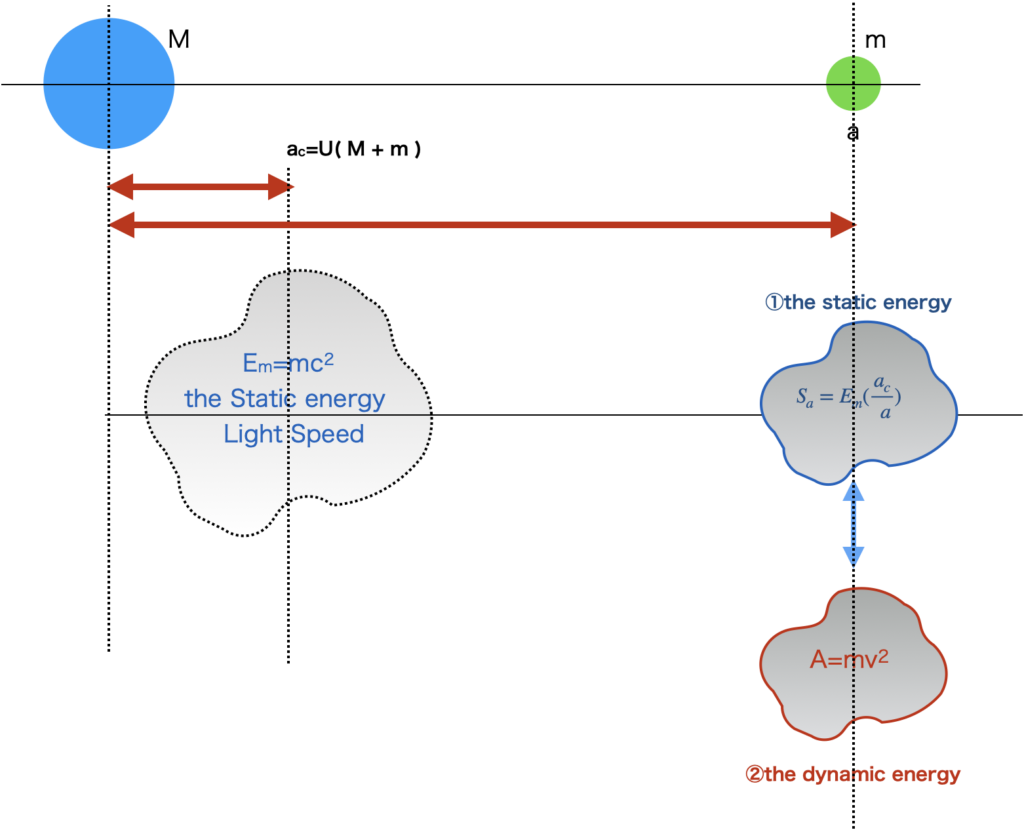
この式を「宇宙エネルギー構造」と呼ぶことにします。左式は距離の比なので、「静的エネルギー」と呼ぶことにします。

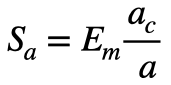
と表します。

右式は速度の比なので、「動的エネルギー」と呼ぶことにします。そして、動的エネルギーは

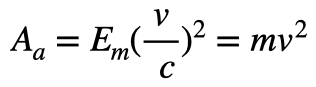
と表します。

Sa=Aaの時バランスして、円軌道になります。

この時のaを「基準軌道半径」と呼びます。

光速時の基準軌道半径(ac)

ところで、光速時の基準軌道半径a_cはどのように表されるでしょうか。

ここで、ニュートンの万有引力の法則を利用します。万有引力が無いと言っておきながら、それを使うのかと言うことですが。

実際ニュートンの万有引力の法則は、通常の速度範囲なら正しいことが証明されています。アインシュタインの重力場とか考えなければですが。とりあえず、ニュートンの万有引力が正しいとすると、ニュートンの万有引力エネルギー変換した、

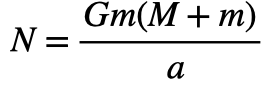
は、距離によって決まるので「静的エネルギー(Sa)」と同値になります。

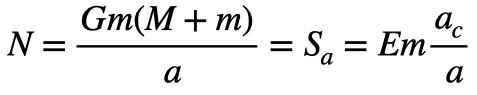
E_m=mc²より、

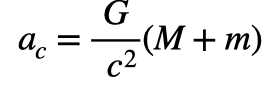
となります。Gは万有引力定数になります。

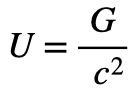
と置いて、Uを宇宙エネルギー定数と呼ぶことにします。（U=7.42426e-31Km/Kg）…１Kgあたりの基準軌道半径(km)

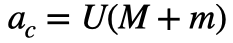
と表します。

従って、光速時の基準軌道半径acは、２天体の質量の和で決まります。

楕円軌道

楕円軌道は、「円軌道」＋「単振動」です。

楕円軌道の原因の一つは、天体同士の衝突です。地心座標をグラフで描くと

「円軌道」の地心座標は、fs=b

「単振動」の地心座標は、f_A=Acos(ωt)　

楕円軌道の地心座標fは、f = fs＋f_A = b + Acos(ωt)　（下グラフの黒線）になります。

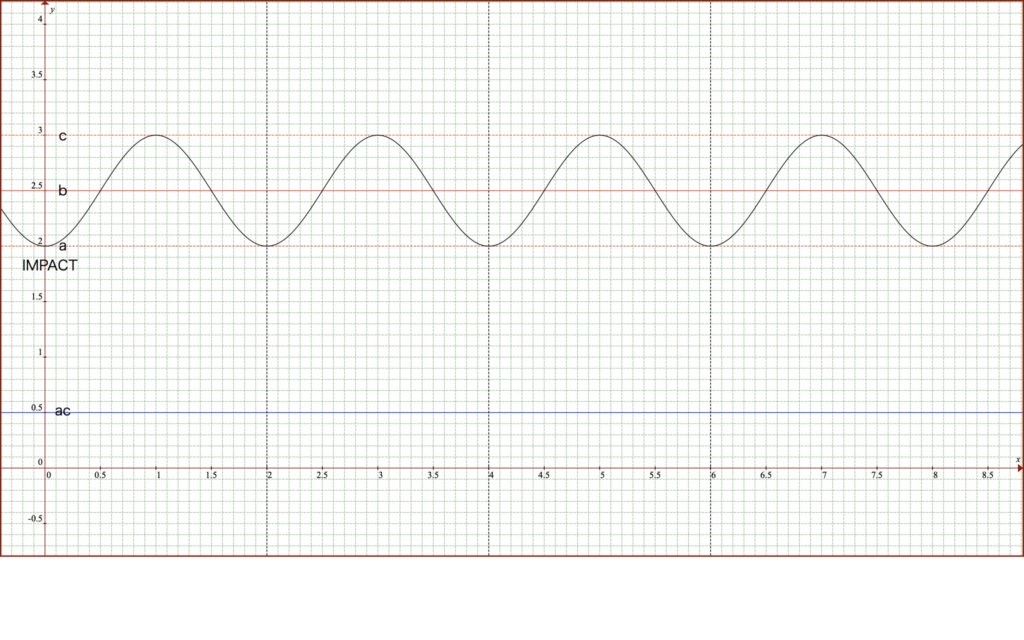
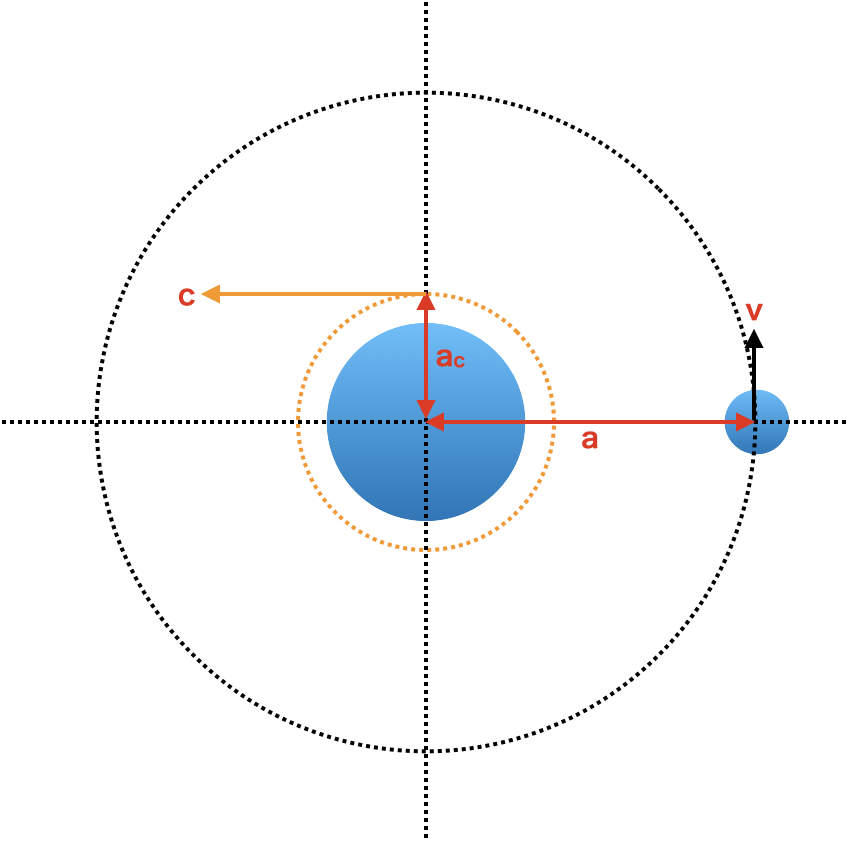
衝突後の軌道ををみてみると、元基準軌道のある位置で衝突が発生すると、静的エネルギーがバランスする、現基準軌道に基準軌道が移ります。その為、現基準軌道を中心に振幅fの振動が発生します。そして、一番遠い点は遠点（c）となり、一番近い点は近点（a…衝突した位置）になります。これは、衝突が周回天体進行方向で起こった場合ですが、周回天体進行の逆方向で衝突した場合は、下図ではc位置で衝突したような軌道になります。原理は同じで、運動エネルギーが減りますので、基準軌道は小さくなります。

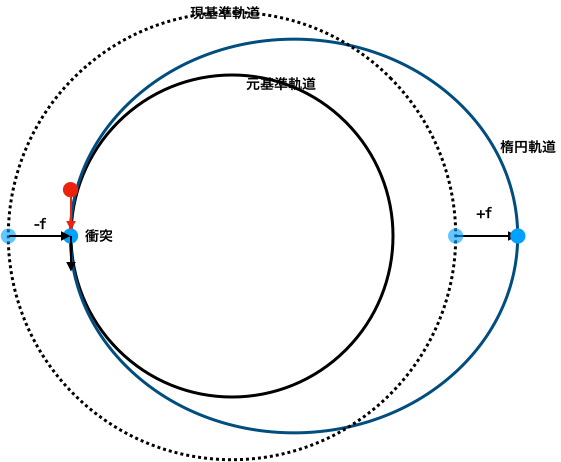
単振動の原理

周回天体は、基準軌道をベースに中心天体の周りを回っています。基準軌道上では、「静的エネルギー」＝「動的エネルギー」になります。この周回天体に他の天体が衝突すると、動的エネルギーが増減する。ここでは増加する時の場合を考えてみます。静的エネルギーは、距離によって決まるので、任意の距離(a)では一定です。そのため、動的エネルギーは静的エネルギーより大きくなり、

静的エネルギー（Sa）＜衝突エネルギー（I）＋　動的エネルギー（Aa）=A’a

になります。

このアンバランスの位置(a)から、静的エネルギー＝動的エネルギーとなるバランスする場所、基準軌道(b)に移動します。衝突エネルギーを減らして静的エネルギー＝動的エネルギーになる位置(b)まで天体が移動します。

静的エネルギーの減衰（下図の青線）は

静的エネルギー(S_a)　-　衝突エネルギー(I)　＝　静的エネルギー(S_b)　となります。

動的エネルギーの減衰（下図の赤線）は

動的エネルギー(A’a) – 2 x 衝突エネルギー(I) = 動的エネルギー(Ab)

a点で衝突してb点が基準軌道になると、bーaの距離、反動でc点まで移動して、また、b点に戻っていく流れを繰り返し単振動します。

この図から、作用反作用がエネルギーに働いていることが推測できます。

衝突から単振動している間、全ての時点で、静的エネルギーを中心に動的エネルギーが±ゼロとなります。

衝突時は、衝突エネルギー（I）の増加分、静的エネルギーに対して、−衝突エネルギー（I）が働くとみなせます。

a点の衝突は周回天体の正方向に衝突した場合です。周回天体進行の逆方向の場合は、c点で衝突が起こった場合です。

単振動周期

周回天体は基準軌道移動により、衝突位置の基準軌道aから衝突後の基準軌道bへの移動するため、移動距離f=b-aが振幅となり、基準軌道bを中心に振幅fの単振動する。この振幅は楕円軌道の中心からの焦点距離に等しい。

単振動の周期TAは、面積エネルギーをEA、衝突後の基準軌道半径をbとすると、基準軌道bで安定するので、バネ定数が 

のバネと見做すことができ、単振動周期は 

(h)となります。

この式から、質量が変化しない限り、円軌道の周期TbとTAは同じになり、円軌道＋単振動で、見かけ上楕円軌道なる。

近点移動

単振動の周期TAは、質量の変化により変化します。

公転周期と単振動周期の差により、近点移動が発生します。

単振動周期と公転周期同一の証明

[h] [je・km-2] m：質量[kg] k：バネ定数[je・km-2] Sa：衝突前静的エネルギー[je] a：基準軌道半径[km] [proof] 静的エネルギーと動的エネルギーがバランスすると、Sa=A=mv2….①と表される ①式の両辺をa2で割ると、 …②となる。 ここで、…③はバネ定数となる。 ②式と③式より …④ →…⑤ ⑤式の両辺に２πをかけると、 …⑥ ⑥式の右辺は公転周期T、左辺は単振動周期（TA）となり、質量m固定の場合は、T＝TAとなり、公転周期と単振動周期は等しくなる。

月の場合、８.８５年で近点が一周回ります。すなわち、月が１回公転すると約３度前進します。

月の周期T1=655h、質量m1=7.35e22 kgとすると３度進むには、５.４時間かかります。(655(h)/360(度) x 3(度))

質量の変化による近点移動により、m₂ = m₁ x ( T₂ / T₁ )²なので、

m₂ = 7.35e²² x ((655 + 5,4)/655)² = 7.47e²² kg

Δm = m₂ – m₁ =1.2e²¹

∴月の質量は、衝突により1.2e21 kg 増加したことになります。

この理論は、水星の近日点移動にも応用できます。

移動先の基準軌道(b)

次は、衝突した後の基準軌道（b）、については次式のように計算できます。

静的エネルギー(S_a)　-　衝突エネルギー(I)　＝　静的エネルギー(S_b)　（S_b = S_a – I　）に　位置bの静的エネルギーS_b = Em(a_c/b)　を代入してbを求めると

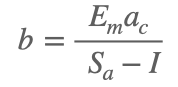
となり、これを基準軌道半径方程式と呼ぶことにします。

E_ma_cは、周回天体の質量　に光速の２乗を乗じたE_mと両天体の質量で決まる光速時基準軌道半径a_cをかけた値なので、中心天体と周回天体の質量が決まれば一意に決まります。

Saは、衝突時の位置aで算出できます。すなわち、衝突エネルギーIがわかれば、どこに基準軌道が移動するかわかります。

衝突エネルギーは、衝突天体の軌道方向の運動エネルギーと解釈できるので、衝突天体の動的エネルギーが分かれば、計算することができます。動的エネルギーは、質量　x 速度^２なので、楕円軌道の大きさがわかれば、衝突天体のある程度の質量と速度を想定することができます。（※下の例で計算してみます）

例.月に仮想天体Xが衝突した場合

当初月は、現在の近地点ap=3.56e⁵kmで円軌道を動いていました。

その位置で他の天体Xと衝突して、現在の軌道になったと仮定します。

衝突天体の衝突エネルギー I = mi x vi²=5.80 e²⁸kg・ km²・h^-2

（衝突天体X　質量mi=3.68e²¹ 衝突速度vi=4.00e³km/hを想定）

と仮定します。

月の移動後の基準軌道位置(b)は、基準軌道半径方程式

= 3.84e³⁵ / (1.06e³⁰ – 5.80e²⁸) = 3.84e⁵ kmとなります。

　　　※E_m a_cは、 mc² x U(M+m) = 3.84e³⁵ kg・ km³・h^-2

　　　Saは、 E_ma_c / a = 1.06e³⁰ kg・ km²・h^-2となりますので、

天体Xが衝突したとすれば、基準軌道が、3.56e⁵km から 現在の3.84e⁵kmに基準軌道移動します。

軌道形態

基準軌道半径方程式で、重要なのは分母がゼロになる時、つまりbが無限大になる時です。つまり、Sa=Iの時です。

これが、親が変わる境界です。それ以上の衝突エネルギーになると、周回天体の親は、中心天体の親（一つ上の親）に変わります。例えば地球の周りを回っている月に、基準軌道の静的エネルギーの大きさ以上の衝突エネルギーが衝突によって供給されると、太陽が親になり太陽の周りを周りを周ります。

実際に、月で実験するわけにはいきませんが、ロケットが第二宇宙速度を得て、地球を脱出する話と同じことです。

軌道形状は、衝突エネルギーの大きさにより（１）大楕円軌道、（２）円軌道、（３）小楕円軌道、（４）落下の４つに分類できる。

ニュートンとケプラーによる放物線、双曲線軌道は、動的エネルギーが静的エネルギーの２倍を超えてしまうので、上位の親に中心天体が移ってしまうため発生しない。

条件	軌道形状	基準軌道b
	Big Ellipse	∞＞b>a
	Circle	a=b
	Small Ellipse	0<b<a
	Fall	b=0（中心天体の中心）

親判定

衝突エネルギーがSa=Iの時、移動後の基準軌道は

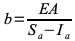
であるから、b=∞になり、親が子を拘束できる範囲を超え、上位の親へ移動します。

これは、子の動的エネルギーA’＝A+Iが2S_aを超えると上位親移動することを意味します。

【親判定の条件】

衝突エネルギーによる判定

条件	親
	上位親
	現在親

動的エネルギーによる判定

条件	親
	上位親
	現在親

I_a：衝突エネルギー[je]

S_a：静的エネルギー[je]

二重衝突ロジック

一回の衝突の軌道の変化は、前項でものべたように、サイン波の楕円軌道になります。そこで、もう一度衝突したらどうなるかということを検討してみました。

ここで例を使って二重衝突のロジックを考察します。

円軌道の軌道周期（例T₀=1000時間）が基準軌道の移動で軌道周期(例T₁=1100時間)に変化しています。もしこの周期(例T₁=1100時間)の見かけ上の楕円軌道天体に、さらに衝突があって基準軌道が移動し軌道周期(例T2=1200時間)になった場合を考えてみます。

まず、楕円軌道の単振動の式をf=Acosωt　とします。ここで三角関数にcosを使ったのはt=0で最大にしたかったためです。

fは振幅位置、

Aは楕円軌道の単振動振幅、

ωは各振動数、

tは時間です。

この式に基準軌道半径a₀を加えたが地心座標になります。

y=Acosωt + a₀

ここで、角振動数ω=2π/Tなので

ω₀=2π/T₀

ω₁=2π/T₁

ω₂=2π/T₂となります。

ω_１とω_２をω_０をベースで表すと、

ω_１＝T₀/T₁ x ω₀

ω₂＝T₀/T₂ x ω₀になります。

ここで、周期の比率α₁=T₀/T₁、α₂=T₀/T₂を周期率とすると

周期の比率（周期率）は、

１回目の衝突の周期率(α₁)はα₁=0.90909

２回目の周期率(α₂)は、α₂=0.83333になります。

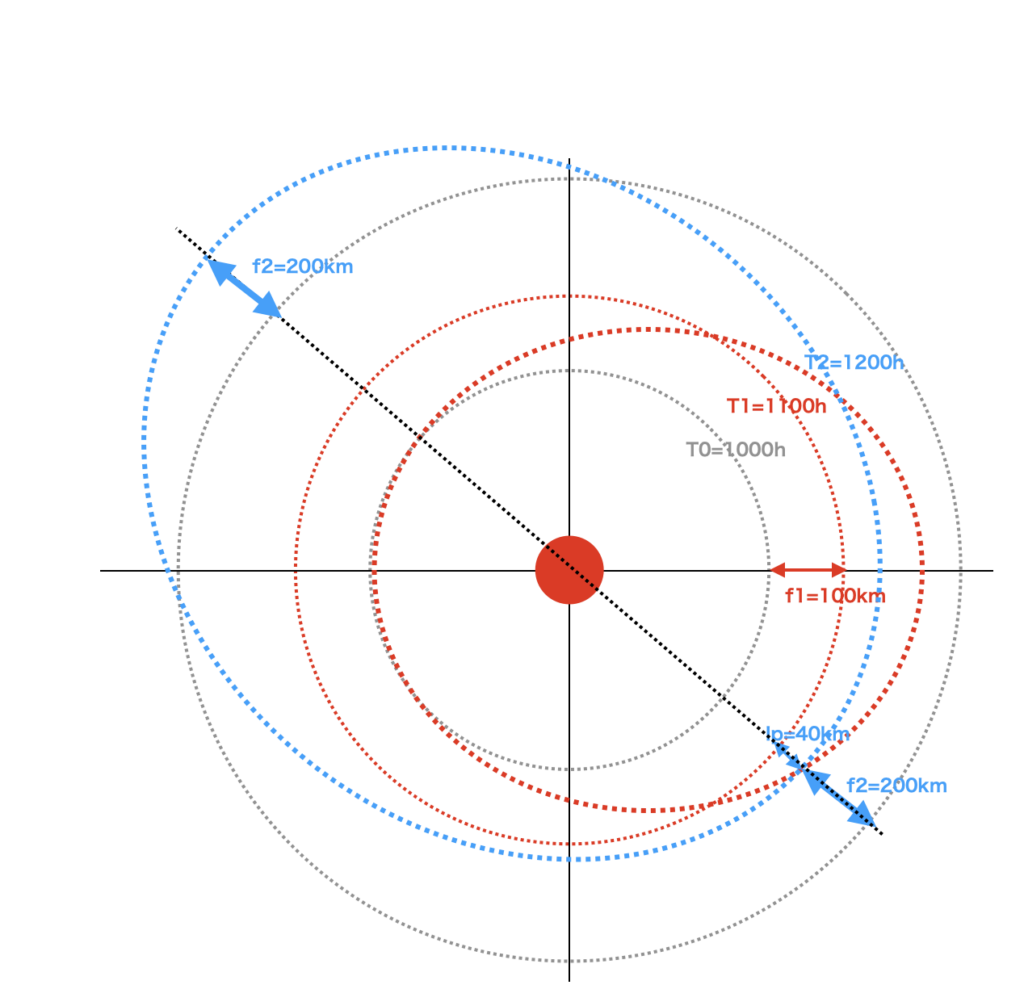
ここで、１回目の衝突の単振動の振幅を100km とすると、１回目の楕円軌道の単振動の式はf₁＝100cos(0.90909ω₀t）となります。

次に2回目の衝突の単振動を200kmとすると、２回目の楕円軌道の単振動の式はf₁の単振動は、角振動数α₂は0.83333、唸り率は0.2になるので、単振動の式は、f₂₁=100cos(0.83333ω₀t)cos(0.2ω₀t）になります。

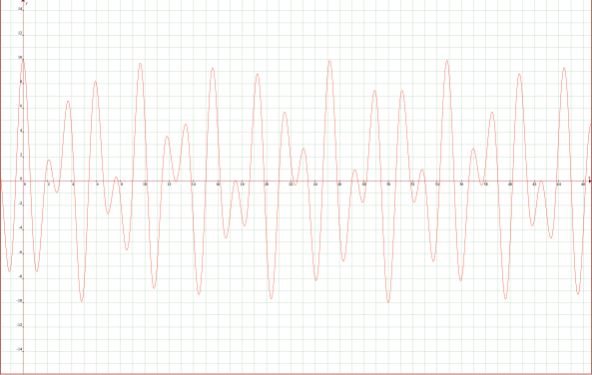
唸り率β₂は、β₂=(T₂-T₀)/T₀で計算します。β2=0.2となりうなりは5回周期で起こることになります。

しかし、第一回目の軌道のどの位置で、衝突したかが問題になります。上の式の場合、基準軌道上で衝突した場合になってしまいます。

そこで、衝突位置を考慮した場合の、基準軌道からの距離を(Ip=40Km)とすると単振動の式は、f₂₁=(100cos(0.83333ω₀t)-40)cos(0.2ω₀t）になります。

しかし、第一回目の軌道のどの位置で、衝突したかが問題になります。上の式の場合、基準軌道上で衝突した場合になってしまいます。そこで、衝突位置を考慮した場合の、基準軌道からの距離を(Ip=40Km)とすると単振動の式は、f₂₁=(100cos(0.83333ω₀t)-40)cos(0.2ω₀t）になります。

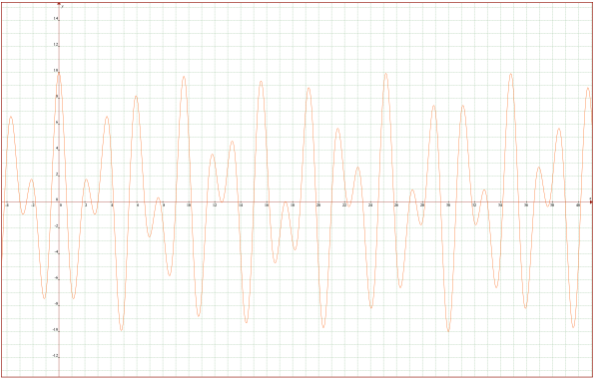
第一回目の軌道は上図のようになります。

第二回目の起動はf22=200cos(0.83333ω₀t)

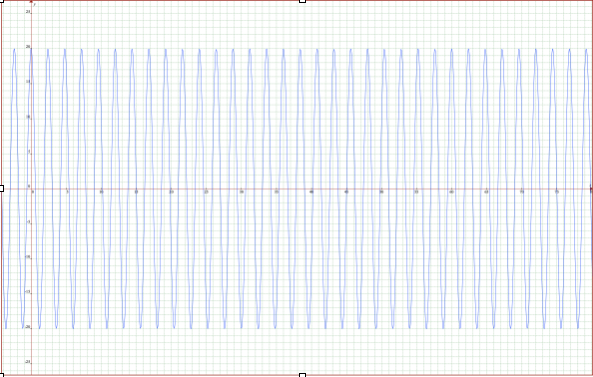
第二回目の衝突の後の軌道f2=f21+f22は次図のようになります。これは第一回目の単振動が基準軌道から４０kmのところで、上下に分割して第二回目の衝突で発生したf₂₂の単振動の遠近点上に合成された形になります。200Kmのところで260Km〜140Kmの範囲で振動、また、-200Kmのところで-240Kmから60Kmの範囲で振動していますこれは、二重衝突による「唸り軌道」と呼ぶことにします。

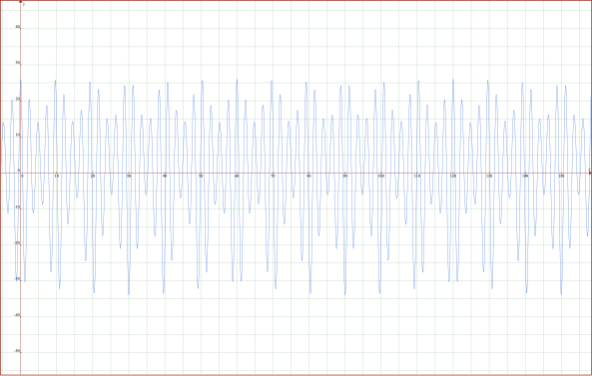
では、ここで月軌道のモデリングデータで計算してみます。

月軌道のモデリング

	軌道形状	基準軌道半径	振幅(f)	衝突位置	軌道周期
当初	円軌道	356,400km	–		584.68h
第１衝突				356,400km
	楕円軌道	360,600km	4,200km		595.04h
第２衝突				363,400km
	楕円軌道	384,400km	21,000km		654.91h

地心座標　第１衝突による　単振動

当初軌道周期　T₀=584.68h第1回軌道周期　T₁=595.04h唸り率　β₂=(T₂-T₀)/T₀=0.12012第1回衝突オフセット　Ip₁=0第2回衝突オフセット　Ip₂=2800=363,400 – 360,600第１衝突振幅　A₁=4,300Km

f₂₁=(A₁cos(α₂ω₀t)-Ip₂)cos(β₂ω₀t)=(4200cos(0.89276ω₀t)-2800)cos(0.12012ω₀t)

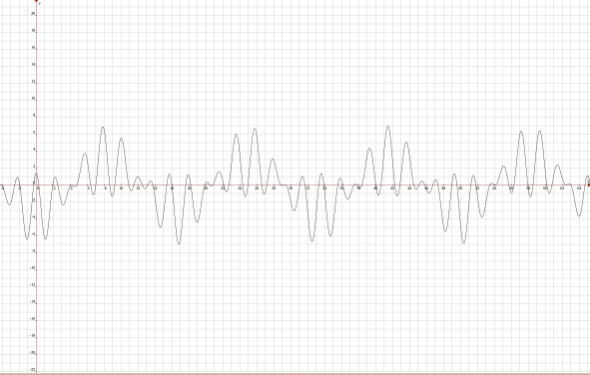
地心座標　第２衝突による　単振動

f₂₂=A₂cos(α₂ω₀t)=21000cos(0.89276ω₀t)

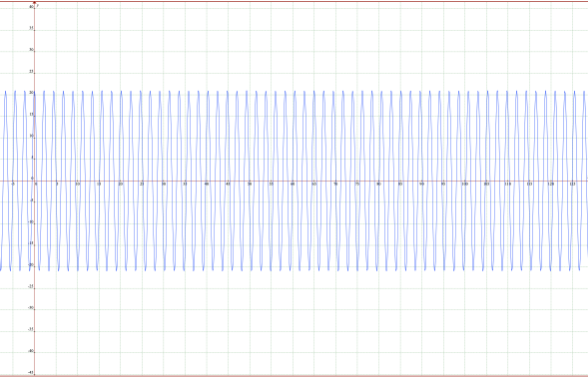
月軌道の地心座標

第１衝突と第２衝突を合成すると　f₂ = f₂₁ + f₂₂

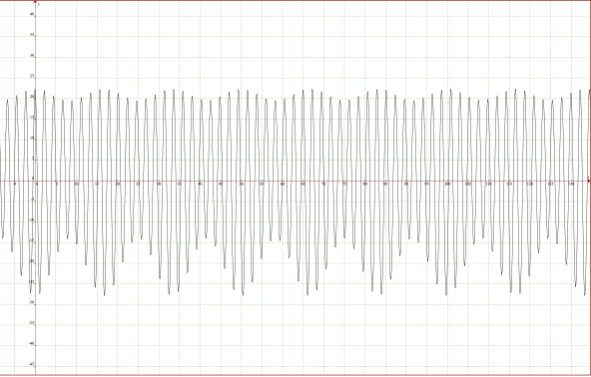
この地心座標は、国立天文台の地心座標のグラフと類似しています。二重衝突がエキセントリックな軌道上を月が移動していると推測できます。これが、月のエキセントリックな軌道の原因です。

そして、重力がなくても、月の軌道が説明できることから、「非重力理論」の仮説は、正しいことになります。